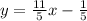Question

write a equation of the line satisfying the giving conditions. write the answer in slope intercept form or standard form. Express numbers as integers or simplified fractions.the line passes (1,2) and (-4,-9)the equation of the line is

Answer 1

The slope intercept form of a line can be expressed by the following equation:

`y=(y_2-y_1)/(x_2-x_1)x+b`

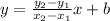
Where (x1, y1) and (x2, y2) are the known points and b is the y-intercept of the line. Using the points provided on the question we have:

`\begin{gathered} y=(-9-2)/(-4-1)x+b \\ y=(11)/(5)x+b \end{gathered}`

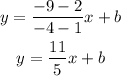
To find the y-intercept we need to apply one of the given points on the expression above.

`\begin{gathered} y=(11)/(5)x+b \\ \\ 2\text{ = }(11)/(5)\cdot1+b \\ b=2-(11)/(5)=(10-11)/(5)=(-1)/(5) \end{gathered}`

The expression for the line is:

`y=(11)/(5)x-(1)/(5)`