Answer:
Step 1:
We will calculate the slope of the line using the formula below
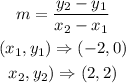
Bu substituting the values, we will have
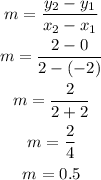
Step 2:
We will represent in the slope-intercept form using the formula below
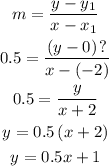
Step 3:
We will represent the equation in point-slope form using the formula below
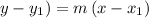
By substituting the values,we will have
![\begin{gathered} \operatorname{\lparen}y-y_1)=m\left(x-x_1\right) \\ y-0=0.5\left(x-\left(-2\right)\right) \\ y-0=0.5\left(x+2\right) \\ \\ \operatorname{\lparen}y-y_2)=m\lparen x-x_2) \\ y-2=0.5\left(x-2\right) \end{gathered}]()
Hence,
The final answers are OPTION B, OPTION C, OPTION D