Question

If the concentration of mercury in the water of a polluted lake is 0.200 μg (micrograms) per liter of water, what is the total mass of mercury in the lake, in kilograms, if the lake has a surface area of 10.5 square miles and an average depth of 53.0 feet?

Answer 1

The total mass of mercury is 86kg.

Step-by-step explanation:

1st) It is necessary to calculate the volume of the lake.

The given information about the lake is:

- Surface: 10.5 square miles

- Depth: 53.0 feet

We have to convert the 10.5 square miles into feet:

`10.5\text{ square miles}*\frac{2.78*10^7\text{ square feet}}{1\text{ square mile}}=2.92*10^8ft^2`

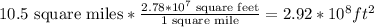
Now we have to multiply the value of the surface by the depth, to calculate the volume of the lake:

`\begin{gathered} Volume=surface*depth \\ Volume=2.92*10^8ft^2*53.0ft \\ Volume=1.5*10^(10)ft^3 \end{gathered}`

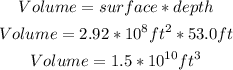
Now we know that the volume of the lake is 1.5x10^10 ft^3.

2nd) Using the volume of the lake and the given concentration of 0.200 μg per liter, we can calculate the total mass of mercury in the lake.

Here it is necessary to convert μg into kg:

`0.200\mu g*(1*10^(-6)g)/(1\mu g)*(1kg)/(1000g)=2*10^(-10)kg`

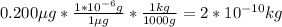
It is also necessary to convert ft^3 to L:

`\begin{gathered} 1ft^3-28.3L \\ 1.5*10^(10)ft^3-x=(1.5*10^(10)ft^3*28.3L)/(1ft^3) \\ x=4.3*10^(11)L \end{gathered}`

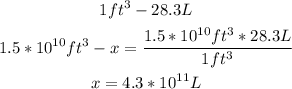
Now with a mathematical rule of three we can calculate the mass of mercury:

`\begin{gathered} 1L-2*10^(-10)kg \\ 4.3*10^(11)L-x=(4.3*10^(11)L*2*10^(-10)kg)/(1L) \\ x=86kg \end{gathered}`

So, the total mass of mercury in the lake is 86kg.