Sales price (x) is the independent variable
Number of Fun Noodles Sold (y) is the dependent variable
Given the two information, we can write 2 coordinate points as shown:

a)
We can use the point slope formula for a line to determine the slope intercept form [y = mx + b]. Shown below:
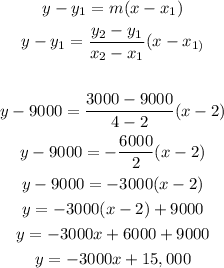
This is the slope intercept form of the line:
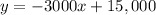
b)
We want to find the sales, y, for sale price, x, of 3.50.
We simply plug 3.5 into x and find the value of y:
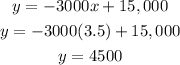
Daily Sales at $3.50 would be around $4500