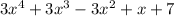Question

Simplify (5x4 – 3x2 + 7x – 10) – (2x4 – 3x3 + 6x – 17)

Answer 1

When adding or subtracting two polynomial expression, we operate with the corresponding coefficients.

`\begin{gathered} (a_nx^n+a_(n-1)x^(n-1)+...+a_1x+a_0)+(b_nx^n+b_(n-1)x^(n-1)+...+b_1x+b_0) \\ =(a_n+b_n)x^n+(a_(n-1)+b_(n-1))x^(n-1)+...+(a_1+b_1)x+(a_0+b_0) \end{gathered}`

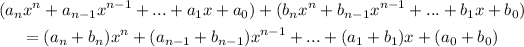
Then, applying this property in our problem, the subtraction between those two polynomials is:

`\begin{gathered} (5x^4-3x^2+7x-10)-(2x^4-3x^3+6x-17) \\ =5x^4-3x^2+7x-10-2x^4+3x^3-6x+17 \\ =(5-2)x^4+(0+3)x^3+((-3)+0)x^2+(7-6)x+((-10)+17) \\ =3x^4+3x^3-3x^2+x+7 \end{gathered}`

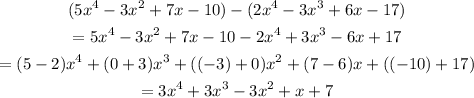
And this is the simplified version of our expression:

`3x^4+3x^3-3x^2+x+7`