The given problem can be exemplified in the following diagram:
To determine the value of the force "F" we need to add the forces in the direction of the inclined plane. Since we want the velocity to stay constant then the acceleration must be zero and therefore, the sum of the forces must add up to zero, therefore, we have:
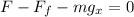
Where:
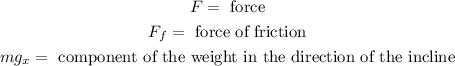
Now we solve for the Force "F" by adding the force of friction and the component of the weight in both sides of the equation:
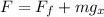
To determine the force of friction we will use the following equation:
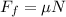
Where:
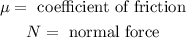
The normal force can be determined by adding the forces in the perpendicular direction of the incline, we get:
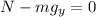
Where:
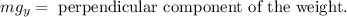
Now we need to determine the components of the weight. To do that we will use the following triangle:
Using the trigonometric function cosine we get:
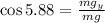
Now we multiply both sides by "mg":
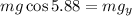
Replacing the values we get:
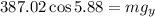
Solving the operations:
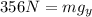
Now we use the trigonometric function sine:
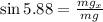
Now we multiply both sides by "mg":
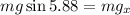
Replacing the values:
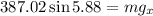
Solving the operations:
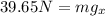
Now we replace the perpendicular component in the formula for the normal:
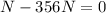
Therefore, the normal force is:
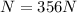
Now we replace the value of the normal force in the formula for the force of friction:
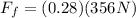
Solving the operation we get:
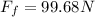
Now we replace in the formula for the force "F":
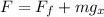
Replacing the values:
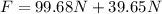
Solving the operations
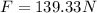
Therefore, the required force is 139.33 Newtons.