Question

Pre calculus Log26x = 1 + 2 log2y1 + log6x = log6 (15y- 25)

Answer 1

Hello there. To solve this simultaneous equation, we'll have to remember some properties about logarithms.

Given the equations:

`\begin{gathered} \log _2(6x)=1+2\log _2(y) \\ 1+\log _6(x)+\log _6(15y-25) \end{gathered}`

First, we'll transform those ones into logarithms applying the following rule in reverse:

`\log _a(a)=1`

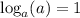
Thus, we get:

`\log _2(6x)=\log _2(2)+2\log _2(y)`

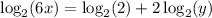
For the first equation; Now, apply the power and product rules in reverse:

`\begin{gathered} \log _c(a^b)=b\cdot\log _c(a) \\ \log _c(ab)=\log _c(a)+\log _c(b) \end{gathered}`

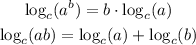
In order to obtain:

`\log _2(6x)=\log _2(2)+\log _2(y^2)=\log _2(2y^2)`

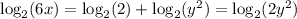
Since both logarithms have the same base, the expressions inside them must be equal as well, therefore:

`\begin{gathered} 6x=2y^2 \\ \\ y^2=3x \end{gathered}`

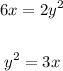
Now, going for the second equation, we'll apply the same three rules as before:

`\begin{gathered} 1+\log _6(x)=\log _6(15y-25) \\ \log _6(6)+\log _6(x)=\log _6(15y-25) \\ \log _6(6x)=\log _6(15y-25) \\ 6x=15y-25 \end{gathered}`

The thing is that we can plug in 6x as y², found on the first equation, to get a quadratic equation for y:

`2y^2=15y-25`

Subtract 15y-25 on both sides of the equation

`2y^2-15y+25=0`

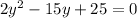
Using the quadratic formula, we take the roots of the equation:

`y=\frac{15\pm\sqrt[]{225-4\cdot2\cdot25}}{2\cdot2}=\frac{15\pm\sqrt[]{25}}{4}=(15\pm5)/(4)`

So we have two possible roots:

y = (15 - 5)/4 = 10/4 = 5/2 or y = (15 + 5)/4 = 20/4 = 5.

Plugging in this value in the first equation, we solve for x:

`\begin{gathered} 6x=2\cdot\mleft((5)/(2)\mright)^2 \\ 6x=2\cdot(25)/(4) \\ x=(25)/(12) \end{gathered}`

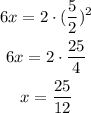
Or

`\begin{gathered} 6x=2\cdot5^2 \\ 6x=2\cdot25=50 \\ x=(25)/(3) \end{gathered}`

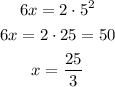
The pair of solutions are:

`\begin{gathered} (x,y)=\mleft((25)/(3),5\mright) \\ (x,y)=\left((25)/(12),(5)/(2)\right) \end{gathered}`

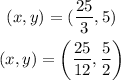
You can plug this into any of the equations and see if they truly satisfy them as an exercise.