Answer
C.
Domain: (-∞, ∞)
Range: [-5, ∞)
Explanation
Given the function:
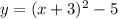
it has the form:
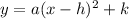
where the constants are: a = 1, h = -3 and k = -5.
This form corresponds to a quadratic function. Given that the function is a polynomial, then its domain is all real numbers.
Given that parameter a is greater than 1, then the parabola opens up. This means that the vertex is the minimum of the function. In the general form, the vertex is the point (h, k), in consequence, in this case, the vertex is the point (-3, -5), that is, on the y-axis the minimum value of the function is y = -5. Therefore, the range of the function is all the numbers greater than or equal to -5.