Question

The points (-18, 15) and (-20,15) lie on a circle with a radius of 1. Find the coordinates of the center of the circle. A C(-18, 15) B. C(-19, 15) C. C(-19, 19) D. C(-20,15

Answer 1

B. (-19, 15)

Step-by-step explanation:

The equation of a circle is generally given as;

`(x-h)^2+(y-k)^2=r^2`

where (h, k) is the coordinate of the center of the circle and r is the radius.

Given the point (-18, 15) and radius of 1, our equation of a circle will become;

`(-18-h)^2_{}+(15-k)^2=1\ldots\ldots...\ldots\ldots\ldots\ldots\text{.Equation 1}`

Given the point (-20, 15), our equation of a circle will become;

`(-20-h)^2+(15-k)^2=1\ldots\ldots\ldots\ldots\ldots..Equation\text{ 2}`

Let's go ahead and subtract Equation 2 from Equation 1, we'll have;

`\begin{gathered} (-18-h)^2-(-20-h)^2+0=0 \\ 324+36h+h^2-400-40h-h^2=0 \\ -76-4h=0 \\ h=-(76)/(4) \\ h=-19 \end{gathered}`

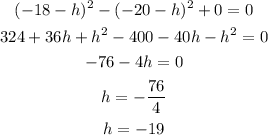
Let's substitute h with -19 in Equation 1 and solve for k;

`\begin{gathered} (-18+19)^2+(15-k)^2=1 \\ 1+(15-k)^2=1 \\ (15-k)^2=0 \\ 15-k=0 \\ -k=-15 \\ k=15 \end{gathered}`

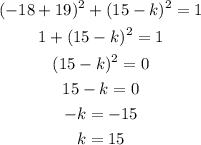
Therefore, the coordinates of the center of the circle is (-19, 15)