The equation of position vs. time for a mass oscilating on a spring with period T is:
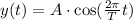
Where A represents the maximum elongation of the spring. The velocity is given by:
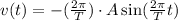
The acceleration is given by:
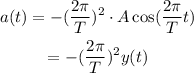
The net force over the mass is equal to its mass times the acceleration:
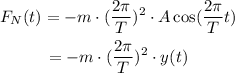
Plot the equations for y(t) and v(t). Use A=1m and T=1.4s:
Position vs. time is shown in red, while velocity vs. time is shown in blue.
The velocity is minimum when the mass reaches the points of maximum elongation, and it is maximum when the mass passes through the equilibrium position (y=0):
Finally, notice that the acceleration and the net force are negative multiples of the position of the mass. Then, the greatest acceleration and the greatest net force are reached when the mass reaches its maximum elongation. The acceleration and the net force will be 0 when the mass passes through the equilibrium position: