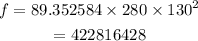Question

The lifting force, F, exerted on an airplane wing varies jointly as the area, A, of the wing's surface andthe square of the plane's velocity, v. The lift of a wing with an area of 280 square feet is 27,800 poundswhen the plarie is going 220 miles per hour. Find the lifting force on the wing if the plane slows downto 130 miles per hour. (Leave the variation constant in fraction form or round to at least 5 decimalplaces. Round off your final answer to the nearest pound.)AnswerHow to enter your answer (opens in new window)5 KeypadKeyboard ShortcutsПіьПЬ

Answer 1

Answer:
`422816428\text{ pounds}`

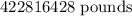
Step-by-step explanation:

Let f be the lifting force.

k be the constant of variation.

a be the area of the wing's surface.

v be the velocity of the plane.

Then

f = 27,800

a = 220

v = 130

Then

`\begin{gathered} f=ka\sqrt[]{2} \\ 27800=k*220\sqrt[]{2} \\ \\ k=\frac{27800}{220\sqrt[]{2}}=89.352584 \end{gathered}`

Since we now know the value of k, we can now solve the problem when

f = ?

a = 280

`\begin{gathered} f=89.352584*280*130^2 \\ =422816428 \end{gathered}`