Question

Lin and Priya were working on solving this system of equations.3x +2y = 4+x + y = -3Lin's first move is to multiply the first equation by 3.Priya's first move is to multiply the second equation by 2.1. Explain why either move creates a new equation with the same solutions as theoriginal equation.2. Whose first move would you choose to do to solve the system? Explain yourreasoning.

Answer 1

Part 1. When we multiply both sides of an equation by the same nonzero number, the equality still holds. Besides, the original e and new equations (after that multiplication) are called equivalent equations, since they have the same solutions.

To see how it works, let's look at this example:

`\begin{gathered} 2x=2 \\ \\ (2x)/(2)=(2)/(2) \end{gathered}`

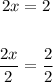
Multiplying both sides by 2, we obtain 4x = 4. And in order to solve this last equation, we need to divide both sides by 4:

`(4x)/(4)=(4)/(4)`

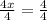
which is the same as:

`\begin{gathered} (2)/(2)\cdot(2x)/(2)=(2)/(2)\cdot(2)/(2) \\ \\ (2x)/(2)=(2)/(2) \end{gathered}`

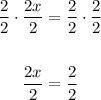
Notice that we naturally get back the original equation in the process of solving the other.

Part 2. Now, comparing the moves of Lin and Priya, we see that Priya's first move produces the equation:

`\begin{gathered} 2\cdot(x+y)=2\cdot(-3) \\ \\ 2x+2y=-6 \end{gathered}`

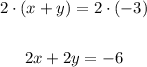
Since 2y also appears in the first equation, we can subtract the one Priyas modified from the first equation to eliminate the variable y and then find x:

`\begin{gathered} 3x+2y-(2x+2y)=4-(-6) \\ \\ x=10 \end{gathered}`

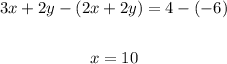
Therefore, the first move that leads to solving the equation faster is Priya's first move.