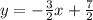Given:
Equation of line
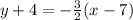
And a point (1,2).
Required:
To find the equation of the line that is parallel to the given line and passes through from the given point.
Step-by-step explanation:
The given equation is:
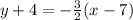
Write the equation in slope-intercept form y= mx+b.
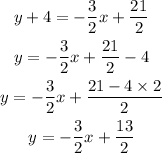
Compare this equation with y=mx+b, we get
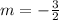
The slope of the parallel lines is equal. So the line that is parallel to the given lime has the same slope.
The equation of line has slope m and passes through from the point
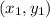
is given by the formula:

Thus the equation of the line passes through from the point (1,2) and has slope m= -3/2 is:
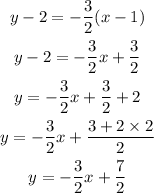
Final Answer:
The equation of the line that is parallel to the given line and passes through from the point (1,2) is