Question

the best basketball player under Kali teen deepthroat on the number of baskets you made on eat less game 11 15 19 12 11 16 11 17 I'll get the mean, median, range, and mid-range of the number of the bus catch you made in her last eight games

Answer 1

Mean, 14; Median, 13.5; Range, 8; Midrange, 15.

Step-by-step explanation:

The mean can be calculated as the sum of all the values divided by the total number of values, so the mean is:

Then, to find the median, we need to organize the numbers from least to greatest, so:

11 11 11 12 15 16 17 19

1st 2nd 3rd 4th 5th 6th 7th 8th

Now, we median will be in the middle of the date, since there are 8 values, the middle is located at position 4.5, so the median is the mean of the number in the 4th position the number in the 5th position, then:

`\text{Median}=(12+15)/(2)=13.5`

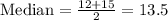
On the other hand, the range is the difference between the greatest value and the least value, so the range is:

`Range=19-11=8`

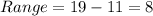
Finally, the midrange is the sum of the greatest value and the least value divided by 2, so:

`\text{Midrange}=(19+11)/(2)=15`

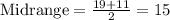
Therefore, the answer is:

Mean, 14; Median, 13.5; Range, 8; Midrange, 15.