Question

Determine if the following equations are parallel, perpendicular, or neither. 4x + 3y = 9 and 6x – 8y = 20

Answer 1

Perpendicular

Explanation:

We have the following equations

`\begin{gathered} 4x+3y=9 \\ 6x-8y=20 \end{gathered}`

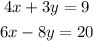
We can determine their relationship by means of the slope, since if the slope is equal they are parallels or if the product of it is equal to -1 they are perpendicular.

Therefore we must calculate the slope of each equation

The equation in its slope-intercept form is as follows:

`\begin{gathered} y=mx+b \\ \text{where m is the slope } \end{gathered}`

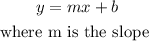
Now, for each equation we solve for y, thus we calculate its slope:

`\begin{gathered} 4x+3y=9\rightarrow y=(9-4x)/(3)\rightarrow y=-(4)/(3)x+3 \\ m=-(4)/(3) \\ 6x-8y=20\rightarrow y=(20-6x)/(-8)\rightarrow y=(3)/(4)x-(5)/(2) \\ m=(3)/(4) \end{gathered}`

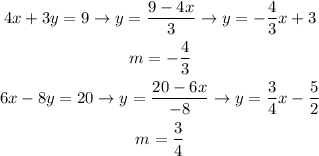
Now, we rerify the relationship between the slopes:

`-(4)/(3)\cdot(3)/(4)=-1`

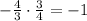
Which means that these equations are perpendicular