Question

How do I find the standard deviation for the following masses?37.3055 g37.4005 g37.4673 g37.3520 g37.5109 g37.3970 g37.4819 g37.2700 g37.3763 g

Answer 1

The sample is given

`37.3055,37.4055,37.4673,37.3520,37.5109,37.3970,37.4819,37.2700,37.3763`

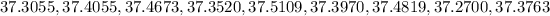
First determine the mean of the sample,

The total number of masses are 9.

Then mean is calculated as sum of all the masses divided by total number of masses.

`(37.3055+37.4055+37.4673+37.3520+37.5109+37.3970+37.4819+37.2700+37.3763)/(9)`
`(336.5614)/(9)=37.39572`

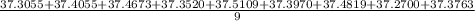
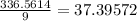
The mean obtained is 37.39572.

To determine the standard deviation , use the formula.

`\sigma=\sqrt[]{(1)/(N)\Sigma(x_i-\mu)^2}`

Now we have to evaluate the value of summation in the square root.

Now substitute the value in standard deviation formula

`\sigma=\sqrt[]{(1)/(9)(0.0520756928)}=\sqrt[]{0.0057861880888}=0.076066997`

Hence the standard deviation of the masses given is 0.076066997.