Question

Sarah took the advertising department from her company on a round trip to meet with a potential client. including Sarah a total of 10 people took the trip. she was able to purchase coach tickets for $240 and first class tickets for $1150. she used her total budget for airfare for the trip which was $9680. How many first class tickets did she buy. how many coach tickets did she buy ?

Answer 1

By the information given in the statement, you can construct the following system of equations.

`\begin{cases}x+y=10\text{ (1)} \\ 240x+1150y=9680\text{ (2)}\end{cases}`

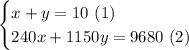
Where

x is the number of coach tickets and

y is the number of first-class tickets

To solve the system of linear equations, you can use the method of reduction or elimination, multiply the first equation by -240, add the equations and solve for the remaining variable.

`\begin{gathered} (x+y)\cdot-240=10\cdot-240 \\ -240x-240y=-2400 \end{gathered}`

Add the equations

`\begin{gathered} -240x-240y=-2400 \\ 240x+1150y=9680\text{ +} \\ -------------- \\ 0x+910y=7280 \\ 910y=7280 \end{gathered}`

Solve for y

`\begin{gathered} \text{ Divide by 910 into both sides of the equation} \\ (910y)/(910)=(7280)/(910) \\ y=8 \end{gathered}`

Now replace the value of y in any of the initial equations, for example in the first

`\begin{gathered} x+y=10\text{ (1)} \\ x+8=10 \\ \text{ Subtract 8 from both sides of the equation} \\ x+8-8=10-8 \\ x=2 \end{gathered}`

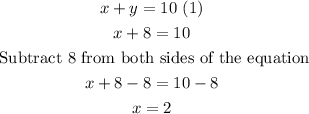
Then, the solutions of the system of linear equations are

`\begin{cases}x=2 \\ y=8\end{cases}`

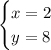
Therefore, Sara bought 8 coach tickets and 2 first-class tickets.