Given: A standard number cube is tossed
To determine: The P(even or prime)
Solution
Step 1: Write the element of the sample space

Step 2: Write the element of even
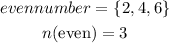
Step 3: Write the elemt of prime
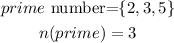
Step 4: Write element of even and prime
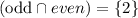
Step 5: Find the P(even or prime)
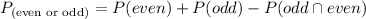
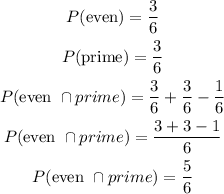
Hence, the probability of even and odd is 5/6