Given:
Line pass through the point ( 4, -1 ) and ( 1, -4 )
Find-:
The slope of the line and graph of the line.
Explanation-:
The slope of the line is:

Where,
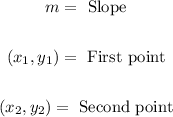
Given point is:
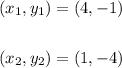
The slope of the line is:

The slope of the line is 1.
For a graph of lines,
Equation of line is:

Where,
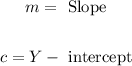
So, the equation become
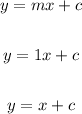
For value of "c" is:
Point = ( 4, -1)

So, the equation

So, the graph of line is: