Question

How many 1 3 inch cubes does it take to fill a box with width 2 inches, length 3 inches, and height 2 1 3 inches? Use the sketch pad to the right to show your thinking. Write your response in the box below.

Answer 1

Given a cube with side l, the volume is given by

`\text{ the volume of cube = }l^3`

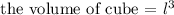
In this case,

`\begin{gathered} l=(1)/(3)\text{ inch} \\ \text{ therefore,} \\ \text{the volume of the cube = (}(1)/(3))^3=(1)/(27)inch^3 \end{gathered}`

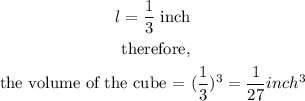
Given a box with width, w, length, l, and height, h, then

`\text{ the volume of the box = }lbh`

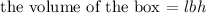
In this case,

`w=2(2)/(3)\text{ inch, }l=3(1)/(3)\text{ inch,}h=2(1)/(3)\text{ inch}`
`\text{ the volume of the box = }2(2)/(3)*3(1)/(3)*2(1)/(3)=(560)/(27)inch^3`

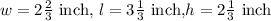
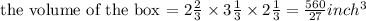
Let the number of cubes it takes to fill the box be n, then we must have

`n=\frac{\text{ volume of the box}}{\text{ volume of the cube}}`
`\begin{gathered} \text{ therefore,} \\ n=((560)/(27))/((1)/(27))=(560)/(27)*(27)/(1)=560 \end{gathered}`

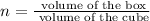
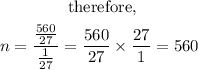
Therefore it will take 560 of the 1 / 3 inch cubes to fill the box