Question

A airplane is traveling north at a indicated airspeed of 110 mph there is a westward cross wind at 13 mph at 90 degrees to the airplane flight path. What is the ground speed of the airplane

Answer 1

Given,

The airspeed of the airplane, v₁=110 mph

The wind speed, v₂=13 mph

The angle between the direction of the wind and the airplane, θ=90°

Let us assume that the northward direction is the positive y-axis and the westward direction is the negative x-axis.

Then the speed of plane and wind in vector representation is,

`\begin{gathered} \vec{v_1}=110\hat{j} \\ \vec{v_2}=13(-\hat{i})=-13\hat{i} \end{gathered}`

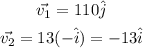
Where i and j are the unit vectors along the x-axis and the y-axis respectively.

The ground velocity of the airplane is the vector sum of the velocity of the plane and the wind. Thus,

`\vec{u}=-13\hat{i}+110\hat{j}`

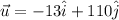
The ground speed of the plane is the magnitude of the vector u, which is,

`\begin{gathered} u=\sqrt[]{(-13)^2+110^2_{}} \\ =110.77\text{ m/s} \end{gathered}`

Thus the ground speed of the airplane is 110.77 m/s