Given;
Admission fee for children is, f(C) = $4.
Admission fee for adult is, f(A) = $5.80.
Total number of people is, N = 296.
Total fees collected is, F = $1472.
The objective is to find the number of children and number of adults.
Consider the childrens as C and the adults as A.
Then, first population equation can be written as,
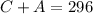
Then, first cost equation can be written as,
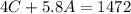
Solve the two equations by multiplying the first equation by 4.
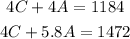
On solving,

Substitute the value of A in equation (1) to finf the value of C.
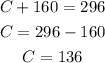
Hence, the number of children is 136 and the number of adult is 160.