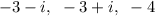You have the folllowing function:
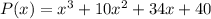
You need to remember the Conjugate zeros theorem, which states that if the polynomial function has a complex zero, then its complex conjugate is also a zero.
Knowing that the following is a zero of the function:
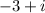
You can determine its conjugate by changing the sign in the middle of the terms. Then:
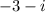
In order to find another possible zero, you can follow the steps shown below. You need to use the Rational root test. Every Rational root will have this form:

Where "p" is a factor of the Constant term and "q" is a factor of the Leading coefficient. Notice that the Leading coefficient is 1.
1. Find the factors of the Constant term. The possible Rational roots are:
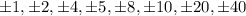
2. Substituting and evaluating, you get:
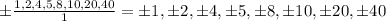
3. Substitute each value into the function and evaluate. If
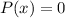
Then that value is a zero of the function.
Therefore, substituting each value into the function, you get:
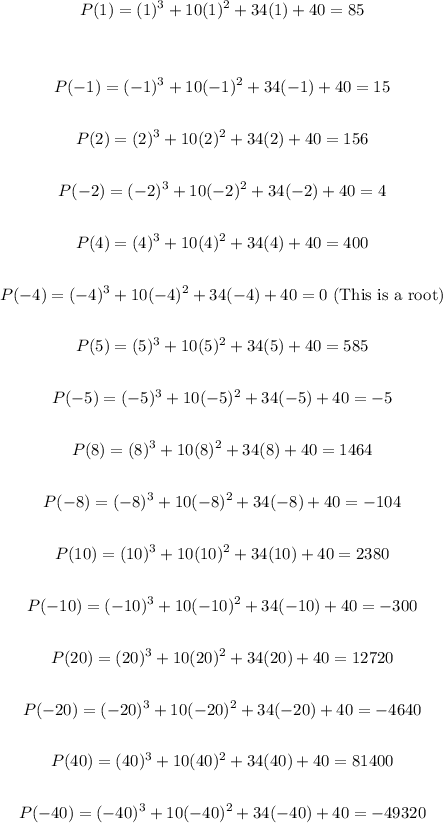
As you can notice, the other root is:
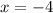
The answer is (The zeros are separated by commas):