Question

9. The expression shown contains a missing coefficient.2y + x + 8y + 24xThe expression is equivalent to 2(5y + 14x).What is the missing coefficient?soOoJOSOOOOOololoOOO O OOOOOOO0 0O O OOOOOOOo

Answer 1

Both expressions are equal:

`2y+ax+8y+24x=2(5y+14x)`

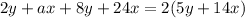
I used the letter "a" to symbolize the missing coefficient, to determine the value of "a", the first step is to solve the multiplication on the parentheses term:

`\begin{gathered} 2y+ax+8y+24x=2\cdot5y+2\cdot14x \\ 2y+ax+8y+24x=10y+28x \end{gathered}`

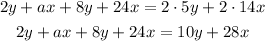
Second, order and simplify the like terms on the left side of the equation:

`\begin{gathered} ax+24x+2y+8y=10y+28x \\ (a+24)x+10y=10y+28x \end{gathered}`

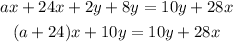
Third, pass "10y" to the right side of the equation by applying the opposite operation "-10y" to both sides of the equal sign:

`\begin{gathered} (a+24)x+10y-10y=10y-10y+28x \\ (a+24)x=28x \end{gathered}`

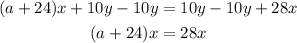
Fourth, note that the terms of both sides are being multiplied by "x", to cancel this multiplication and simplify this variable you have to apply the opposite operation to both sides of the equation. This means that you have to divide the expression by "x"

`\begin{gathered} ((a+24)x)/(x)=(28x)/(x) \\ a+24=28 \end{gathered}`

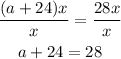
Finally, subtract 24 to both sides of the equal sign to determine the value of "a"

`\begin{gathered} a+24-24=28-24 \\ a=4 \end{gathered}`

The missing coefficient is a=4