Given:
Total number of calls over the last 3 evenings = 108
Number of calls on the third evening = 4 times as many as the first evening
Number of calls on the second evening = 6 fewer calls than the first evening
Let's find the number of phone calls she received each evening.
Let x represent the number of phone calls she received on the first evening
Let y represent the number of phione calls she received on the second evening
Let z represent the number of phone calls she received on the third evening.
Thus, we have:
• Calls on first evening = x
• Calls on second evening = x - 6
• Calls on the third evening = 4x
Since the total number of calls received is 108, we have the equation:
x + (x - 6) + 4x = 108
Let's solve for x:
x + x - 6 + 4x = 108
Combine like terms:
x + x + 4x - 6 = 108
6x - 6 = 108
Add 6 to both sides:
6x - 6 + 6 = 108 + 6
6x = 114
Divide both sides by 6:
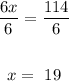
To find the number of calls she received each evening, substitute 19 for x in each expression.
Thus, we have:
Number of phone calls the first evening: x = 19
Number of phone calls the second evening: x - 6 = 19 - 6 = 13
Number of phone calls the third evening: 4x = 4(19) = 76
ANSWER:
• Number of phone calls the first evening = 19
,
• Number of phone calls the second evening = 13
,
• Number of phone calls the third evening = 76