The distance travel by each bus is given by:
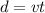
where v is velocity of the bus (the rate of the bus).
We know that one of the buses travels 13 mph slower than the other that means that, if the velocity of the faster bus is v, the velocity is:

Now, the distance travel by each bus after 4 hours is:
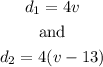
We also know that after this time the total distance between the buses is 596 miles, then:
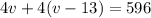
Solving for v we have:
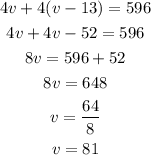
Therefore:
Rate of the slower bus: 68 mph
Rate of the faster bus: 81 mph