Question

Hey could I get sum assistance with this learning exercise sand a brief explanation, thanks

Answer 1

The rule of the sum of n terms in the arithmetic sequence is

`S_n=(n)/(2)[2a+(n-1)d]`

a is the 1st term

d is the common difference

n is the number of the terms

The given sequence is

`9,14,19,24,29,34,.....`

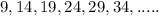
Since

`\begin{gathered} 14-9=5 \\ 19-14=5 \\ 24-19=5 \end{gathered}`

Then the common difference is 5

d = 5

Since the 1st term is 9, then

a = 9

Since we need to find the sum of 23 terms, then

n = 23

Substitute these values in the rule above

`\begin{gathered} S_(23)=(23)/(2)[2(9)+(23-1)(5)] \\ \\ S_(23)=(23)/(2)[18+110] \\ \\ S_(23)=(23)/(2)[128] \\ \\ S_(23)=1472 \end{gathered}`

The sum of the first 23 terms is 1472

The answer is d