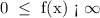![\begin{gathered} a)\text{ Domain; -}\infty<p>Here, we want to get the domain and range of the given functions</p><p></p><p>When we talk of the domain, we are referring to the possible x-values while when we talk of range, we are talking about the possible y-values</p><p></p><p>We have for each of the functions as follows;</p><p></p><p>a) The domain of the relation spans from negative infinity to positive infinity</p><p></p><p>We have this as;</p><p></p>[tex]-\infty\text{ < x < }\infty]()
The range of the function is;
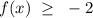
b) For this function, we can see the domain from -2 to 2
In interval notation, this is;
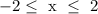
The range of this function as we can see is from 0 to infinity
We have the interval notation as;
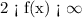
c) For this function, we have;
Domain starts from -4 and extends toward infinity
We have this as;
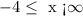
For the range, we have this as;