Question

Me and Mrs.kim hope to send their daughter to college in eleven years. How much money should they invest now at an interest rate of 9% per year, compounded continuously, in order to be able to contribute 7500 to her education? Do not round any intermediate computations; round your answer to the nearest cent

Answer 1

You have to find how much money they should invest to have a balance of $7500 after eleven years, given that the account compounds continuously with a yearly interest rate of 9%.

To calculate the accrued amount of an account that compounds continuously you have to apply the following formula:

`A=Pe^(rt)`

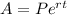
Where

A is the accrued or final amount.

P is the principal or initial amount.

e is the natural number.

r is the interest rate expressed as a decimal value.

t is the time period expressed in years.

To calculate the initial amount P, first write the equation for the variable you want to study:

`\begin{gathered} A=Pe^(rt) \\ Divide\text{ }by\text{ }e^(rt) \\ (A)/(e^(rt))=(Pe^(rt))/(e^(rt)) \\ (A)/(e^(rt))=P \end{gathered}`

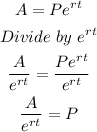
- Divide the interest rate by 100 to express it as a decimal value:

`\begin{gathered} r=(R)/(100) \\ r=(9)/(100) \\ r=0.09 \end{gathered}`

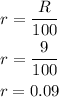
Using A=7500, r=0.09 and t=11 calculate the initial amount P:

`\begin{gathered} P=(A)/(e^(rt)) \\ P=(7500)/(e^(0.09*11)) \\ P=(7500)/(e^(0.99)) \\ P=2786.825\cong2786.83 \end{gathered}`

Mr. and Ms. Kim have to invest $2,786.83 to be able to contribute $7,500 to their daughter's education.