Question

Assume that population mean is to be estimated from the sample described . Use the sample results to approximate the margin of error and 95% coincidence interval N=36, x=59.9 seconds, s=4.3 seconds

Answer 1

Statement Problem: Assume that the population mean is to be estimated from the sample described. Use the sample results to approximate the margin of error and 95% coincidence interval.

`n=36,\bar{x}=59.9\sec ,s=4.3\sec`

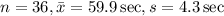
Solution:

The margin of error can be approximated using the formula;

`\begin{gathered} MOE_(\gamma)=z_(\gamma)*\sqrt[]{(\sigma^2)/(n)} \\ z_(\gamma)=1.96_{} \\ \sigma=4.3 \\ n=36 \end{gathered}`

Thus;

`\begin{gathered} MOE_(\gamma)=1.96*\sqrt[]{(4.3^2)/(36)} \\ MOE_(\gamma)=1.4047 \end{gathered}`

Then, we would approximate to one decimal place, we have;

The margin of error is;

`MOE_(\gamma)=1.4`

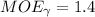
CORRECT ANSWER: 1.4 seconds