Question

Groups of adults are randomly selected and arranged in groups of three. The random variable x is the number in the group who say that they would feel comfortable in a self-driving vehicle. Determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied.

Answer 1

Given the table, we have:

Add all probabilities

0.366 + 0.427 + 0.180 + 0.027 = 1

The table describes a probability distribution because all probabilities are between 0 and 1, and the sum of probabilities is equal to 1.

For mean:

`\begin{gathered} mean=0(0.366)+1(0.427)+2(0.180)+3(0.027) \\ =0.427+0.360+0.081 \\ =0.868 \end{gathered}`

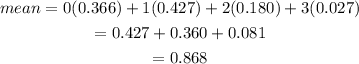
For standard deviation:

`SD=√(0.366(0-0.868)^2+0.427(1-0.868)^2+0.180(2-0.868)^2+0.027(3-0.868)^2)`

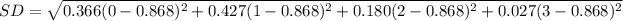
Simplify:

`\begin{gathered} SD=√(0.366(-0.868)^2+0.427(0.132)^2+0.180(1.132)^2+0.027(2.132)^2) \\ SD=√(0.636576) \\ SD=0.798 \end{gathered}`

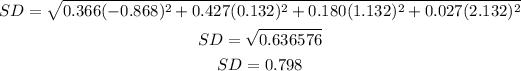
Answer:

Yes, the table shows a probability distribution

mean = 0.868

standard deviation = 0.798