Question

The function f(x) = 4(0.5)* gives the remaining amount, in grams, of a radioactive substance after thesubstance has been decaying for x minutes. What does the equation f(4) = 0.25 represent in thissituation? (FIF.2)A) After decaying for 15 seconds, there are 4 grams of the substance remainingB) After decaying for 25 seconds, there are 4 grams of the substance remainingC) After decaying for 4 minutes, there is 0.25 gram of the substance remainingD) After decaying for 4 minutes, there is 0.25 of the original mount of the substance remaining

Answer 1

c)After decaying for 4 minutes, there is 0.25 gram of the substance remaining

Step-by-step explanation

Exponential growth or decay function is a function that grows or shrinks at a constant percent growth rate,The equation can be written in the form

Step 1

a)What does the equation f(4) = 0.25 represent in this situation?

as the independent variable is the time (x), and the dependent varialbe is the remaining amount of substance,

the expression

`f(4)=0.25`

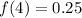
tells us that after 4 minutes the amount of substance is 0.25 grams,

so, the answer is

c)After decaying for 4 minutes, there is 0.25 gram of the substance remaining

I hope this helps you