Question

Dr. Heinz Doofenshmirtz built a springinator to trap Perry the Platypus. Perry finesses his way in with his ninja skills and launches the springinator to Doofenshmirtz instead, hurling him 1500 cm into the air. If he has a mass of 65 kg and the spring's k constant is 1025 N/m, how much was the spring compressed?

Answer 1

The compression in the spring is 4.31 m

Given data:

The mass of Perry is m=65 kg.

The distance traveled in air is h=1500 cm.

The spring constant is k=1500 N/m.

The amount of spring compression can be calculated by equating the gravitational potetial energy equal to the elastic potential energy of the spring. It can be applied as,

`\begin{gathered} \text{GPE}=\text{EPE} \\ \text{mgh}=(1)/(2)kx^2 \\ x=\sqrt{(2mgh)/(k)} \end{gathered}`

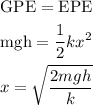
Here, x is the compression in the spring, and g is the gravitational acceleration.

The distance traveled in meters will be,

`\begin{gathered} h=1500cm*\frac{1\text{ m}}{100cm} \\ h=15\text{ m} \end{gathered}`

Substitute the given values in above equation,

`\begin{gathered} x=\sqrt[]{(2(65)(9.8)(15))/(1025)} \\ x=4.31\text{ m} \end{gathered}`

Thus, the compression in the spring is 4.31 m.