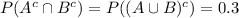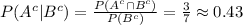Question

Hi am having problems with number 8 can you help please

Answer 1

We can use a diagram to help us visuallize the situation:

Since the middle part is the intersection of A and B, if we add the probability of events A and B, we will add the intercetion twice, so we can remove one of the intercetions to get the total probability inside the circles. This is equivalent of the union of A and B, which is item b:

`\begin{gathered} P(A\cup B)=P(A)+P(B)-P(A\cap B) \\ P(A\cup B)=0.6+0.3-0.2 \\ P(A\cup B)=0.7 \end{gathered}`

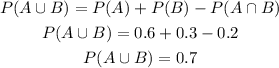
To calculate P( A | B ) and P( B | A ), we need to consider the event of the first give the second have happened.

So, for the first, P( A | B ), we know B have happend, so we are already inside circle B. The part that can occure A is the intercetion only, so this probability is the probability of the intersection over the probability of B:

`P(A|B)=(P(A\cap B))/(P(B))=(0.2)/(0.3)=(2)/(3)\approx0.67`

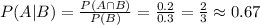
Similarly, the probability P( B | A ) is the intersection over the probability of A:

`P(B|A)=(P(A\cap B))/(P(A))=(0.2)/(0.6)=(1)/(3)\approx0.33`

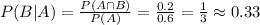
Now, for c, we want the complementaries. Since the total probability is 100%, that is, 1, the sum of the probabilities of the event and its complementay is always 1, so:

`\begin{gathered} P(A)+P(A^c)=1 \\ P(A^c)=1-P(A) \\ P(A^c)=1-0.6 \\ P(A^c)=0.4 \end{gathered}`

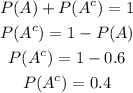
And:

`\begin{gathered} P(B)+P(B^c)=1 \\ P(B^c)=1-P(B) \\ P(B^c)=1-0.3 \\ P(B^c)=0.7 \end{gathered}`

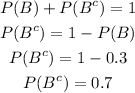
d. Now, we can use the formula we already know and used in a, but now using the complementary probabilities we calulated in c, but first we need the interception of the complementaries.

Back to the diagram, the complementary of the of A is all but the circle A. The complementay of B is all but the circle B. Starting from all, the intersection of the complementaries is only the area around the circles, that is the intersection of the complementaries is the complementary of the union we calculated in b.

So:

`\begin{gathered} P(A^c\cap B^c)=P((A\cup B)^c) \\ P(A^c\cap B^c)=1-P(A\cup B) \\ P(A^c\cap B^c)=1-0.7 \\ P(A^c\cap B^c)=0.3 \end{gathered}`

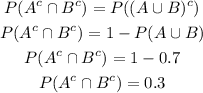
Now, we have all we need to anser the last two. The formual is the one from a but switching to complementaries:

`\begin{gathered} P(A^c|B^c)=(P(A^c\cap B^c))/(P(B^c)) \\ P(A^c|B^c)=(0.3)/(0.7)=(3)/(7)\approx0.43 \end{gathered}`

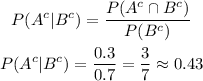
And e:

`\begin{gathered} P(B^c|A^c)=(P(A^c\cap B^c))/(P(A^c)) \\ P(B^c|A^c)=(0.3)/(0.4)=(3)/(4)=0.75 \end{gathered}`

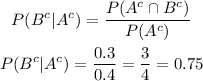
So, summarizing the results and formulas:

a:

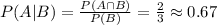
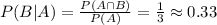
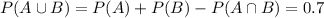
`P(A|B)=(P(A\cap B))/(P(B))=(2)/(3)\approx0.67`
`P(B|A)=(P(A\cap B))/(P(A))=(1)/(3)\approx0.33`

b:

`P(A\cup B)=P(A)+P(B)-P(A\cap B)=0.7`

c:

`P(A^c)=1-P(A)=0.4`
`P(B^c)=1-P(B)=0.7`

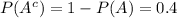
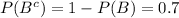
d and e:

`P(A^c\cap B^c)=P((A\cup B)^c)=0.3`
`P(A^c|B^c)=(P(A^c\cap B^c))/(P(B^c))=(3)/(7)\approx0.43`
`P(B^c|A^c)=(P(A^c\cap B^c))/(P(A^c))=(3)/(4)=0.75`