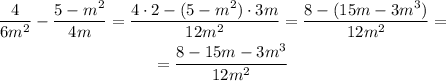
B. The domain of a function is the set that contains every possible value for the independent variable (in this case, m). Given that you cannot divide by zero then
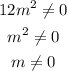
Then, the domain is all real numbers except zero.
C. The expression in the denominator must be set equal to zero because you can't divide by zero.