The question requires us to simplify the polynomials and then affix the right values in the table.
#1:
The polynomial is:

Let us multiply out the bracket and simplify:
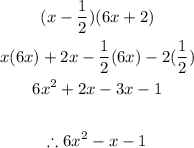
The simplified form is given below:
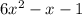
Its degree is quadratic.
There are 3 terms therefore, it is a trinomial
#2:
The polynomial is:
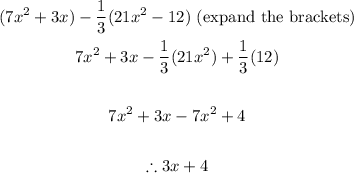
The simplified form is: 3x + 4
Its degree is linear
There are 2 terms therefore, it is binomial
#3:
The polynomial is:

The simplified form is: 2
Its degree is 0 i.e. a Constant
There is only 1 term, therefore, it is Monomial