Question

Could I please get help with this. For ism confused as I have tried multiple times to get the correct answers

Answer 1

item (a):

To find if those figures are congruent, we can just compare the measures of the corresponding sides. Both smaller bases are 1 unit wide, both bigger basis are 2 units wide, therefore, those trapezoids are congruent.

item (b):

To answer this item, let's analyze each transformation individually. Figure A vertices are

`\lbrace(-5,-4),(-2,-4),(-2,-2),(-3,-2)\rbrace`

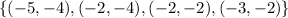
and Figure B vertices are

`\lbrace(5,-2),(2,-2),(2,-4),(3,-4)\rbrace`

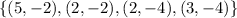
On the first transformation, we have a translation 6 units up, then a rotation counterclockwise of 180º. To do a translation 6 units up, we add 6 to the y-coordinate of each vertice.

`(x,y)\rightarrow(x,y+6)`

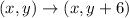
Doing this transformation on figure A, we have

`\begin{gathered} \lbrace(-5,-4),(-2,-4),(-2,-2),(-3,-2)\rbrace \\ \rightarrow\lbrace(-5,-4+6),(-2,-4+6),(-2,-2+6),(-3,-2+6)\rbrace \\ =\lbrace(-5,2),(-2,2),(-2,4),(-3,4)\rbrace \end{gathered}`

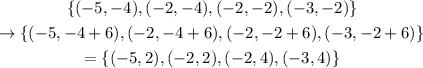
The rule for a rotation by 180° about the origin is

`(x,y)\rightarrow(-x,-y)`

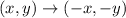
Doing this transformation on the image after the translation, we have

`\lbrace(-5,2),(-2,2),(-2,4),(-3,4)\rbrace\rightarrow\lbrace(5,-2),(2,-2),(2,-4),(3,-4)\rbrace`

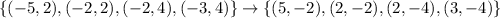
And those are the coordinates of Figure B, thus, a translation 6 units up and then a rotation counterclockwise of 180º around the origin takes Figure A to Figure B.

The second transformation is a translation 8 units up

`\begin{gathered} \lbrace(-5,-4),(-2,-4),(-2,-2),(-3,-2)\rbrace \\ \rightarrow\lbrace(-5,-4+8),(-2,-4+8),(-2,-2+8),(-3,-2+8)\rbrace \\ \lbrace(-5,4),(-2,4),(-2,6),(-3,6)\rbrace \end{gathered}`

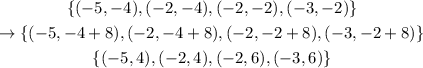
and then, a reflection over the y-axis. The rule for a reflection over the y-axis is

`(x,y)\rightarrow(-x,y)`

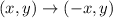
Doing this transformation on the previous figure, we have

`\lbrace(-5,4),(-2,4),(-2,6),(-3,6)\rbrace\rightarrow\lbrace(-5,-4),(-2,-4),(-2,-6),(-3,-6)\rbrace`

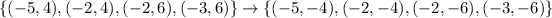
The final figure is NOT figure B. This series of transformations doesn't take figure A to figure B.

The third series of transformation are a reflection on the x-axis, and then a translation 7 units to the right.

The rule for a reflection over the x-axis is

`(x,y)\rightarrow(x,-y)`

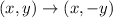
Using this transformation on figure A, we have

`\begin{gathered} \lbrace(-5,-4),(-2,-4),(-2,-2),(-3,-2)\rbrace \\ \rightarrow\lbrace(-5,4),(-2,4),(-2,2),(-3,2)\rbrace \end{gathered}`

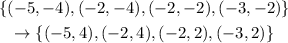
And then, a translation 7 units to the right

`\begin{gathered} \lbrace(-5,4),(-2,4),(-2,2),(-3,2)\rbrace \\ \rightarrow\lbrace(-5+8,4),(-2+8,4),(-2+8,2),(-3+8,2)\rbrace \\ =\lbrace(3,4),(6,4),(6,2),(5,2)\rbrace \end{gathered}`

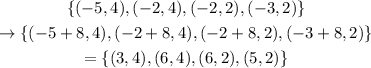
The final figure is NOT figure B. This series of transformations doesn't take figure A to figure B.

And finally, the last transformation is a 90º clockwise rotation, and then translate the figure 6 units to the right.

The rule for a 90º clockwise rotation is

`(x,y)\rightarrow(-y,x)`

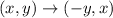
Doing this transformation on figure A, we have

`\begin{gathered} \lbrace(-5,-4),(-2,-4),(-2,-2),(-3,-2)\rbrace \\ \rightarrow\lbrace(4,-5),(4,-2),(2,-2),(2,-3)\rbrace \end{gathered}`

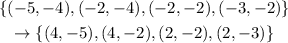
Then, a 6 units translation to the right

`\begin{gathered} \lbrace(4,-5),(4,-2),(2,-2),(2,-3)\rbrace \\ \rightarrow\lbrace(4+6,-5),(4+6,-2),(2+6,-2),(2+6,-3)\rbrace \\ =\lbrace(10,-5),(10,-2),(8,-2),(8,-3)\rbrace \end{gathered}`

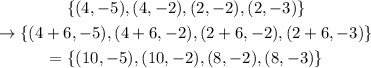
And those are not the coordinates for Figure B.

The only translation from this list that takes Figure A to Figure B is the first option.

"Translate Figure A up 6 units, and then rotate that result counterclowise 180º about the origin"