Ok, so
First of all, remember that the equation of any circumference has the form:
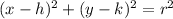
Where:
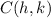
Is the center, and r is the radius.
In this problem, we got that the center of the circumference is located in the point (7 , -24). We also know that this circumference passes through the origin.
Remember that the radius, is the distance from the center of the circumference, to any point of it. In this case, to find the radius, we have to find the distance between the points (7,-24) and (0,0), using the following formula:
Given two points:
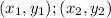
The distance between them is given by:
![D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/bn18956xdzpj56va064oiuu2531qoyd8xa.png)
If we replace our values, we got that:
![\begin{gathered} D=\sqrt[]{(0-(-24))^2+(0-7)^2} \\ D=\sqrt[]{(24)^2+(-7)^2} \\ D=\sqrt[]{576+49} \\ D=\sqrt[]{625} \\ D=25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gs8gh1myuwyc6dizo9g8z7tvcrsqqfdvm6.png)
We got that the distance is 25, so, the radius is 25.
Then, replacing in the general equation of a circumference:
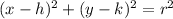
(Our values are):
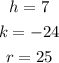
This is;
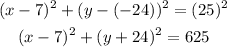
Therefore, the correct answer is C. (x−7)^2+(y+24)^2=625