We are given that BC has one endpoint B(3, 2) and a midpoint T(6, -2)
We are asked to find the coordinates of the other endpoint C.
Recall that the midpoint formula is given by
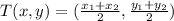
Where

So, the other endpoint C is
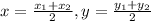
Substitute the given values,
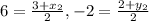
Simplify,
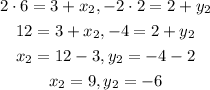
Therefore, the coordinates of the endpoint C are
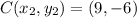
Bonus:
Let us verify whether we got the correct coordinates or not.
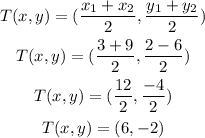
Hence, we got the same midpoint as given in the question.