We want to find the inverse of the following function
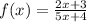
To find the expression of f^-1(x) we begin by changing f(x) for y. So we get
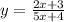
Now, we interchange x and y variables. So we get
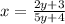
The goal is to solve this equation for variable y. We begin by multiplying both sides by 5y+4. So we get
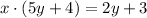
Now we subtract 2y on both sides, so we get
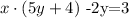
Now we distribute the product on the left, so we get
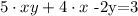
Now we group the terms that have the y variable and factor it out. So we get

now, we subtract 4x on both sides, so we get
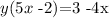
Finally, we divide both sides by 5x-2. We get

Now, we replace y with f^-1(x). So we get
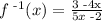
this means that the numerator of f inverse is 3 -4x and the denominator of f inverse is 5x-2