Question

Given the point (3,-4) on the graph of y = f(x), what are the coordinates of the new point after the following transformation: y = -3f(x-2) +6 ? h

Answer 1

We will investigate the application of transformation functions on coordinates.

We will classify the following transformations and their rules required:

Translation:-

It can be associated with either vertical or horizontal shifts of the funtion f ( x ) in a cartesian coordinate plane. The transformation function associated with translations can be generalized as follows:

`y\text{ = f ( x + a ) + b}`

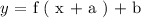
Where,

`\begin{gathered} a>\text{ 0 }\ldots\text{ Left shift} \\ a<0\ldots\text{ Right shift} \\ \\ b>0\ldots\text{ Upward shift} \\ b<0\ldots\text{ Downward shift} \end{gathered}`

The coordinate transformation rule that is applicable for all translations is as follows:

`(\text{ x , y ) }\to\text{ ( x + a , y + b )}`

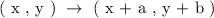
Where,

`\begin{gathered} a\colon\text{ The units of horizontal shift ( left or right )} \\ b\colon\text{ The units of vertical shift ( up or down )} \end{gathered}`

Dilation:-

It is the measure of the amount of stretch or compression that the original function f ( x ) has undergone relative to the point of reference usually its own center as follows:

`y\text{ = c}\cdot f(x)`

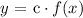
Where,

[tex]\begin{gathered} c>\text{ 1 }\ldots\text{ Enlargement} \\ 0The coordinate rule applicable to the transformation of dilation is: