Given:
p = 47% = 0.47
n = 6
Required:
The probability that at least 4 are using their smartphones in meetings or classes.
Solution:
The binomial probability is defind as :
We will use this definition to solve for P at X = 4, X = 5 and X = 6 (since the probability of at least 4 users is asked)
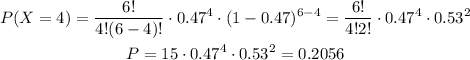
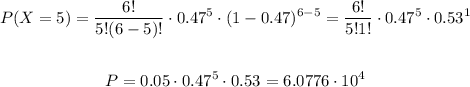
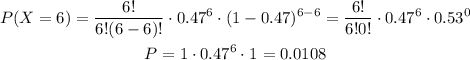
![undefined]()