Question

MetroTran had a route reduction and lost 1/5 of its routes. If 88 of its routes were left after the reduction, how many routes were there originally?

Answer 1

Step 1: Represent the total original routes with an unknown

Let the total original route be x

Step 2: Represent the first statement with a mathematical expression

`\begin{gathered} \text{The loss is 1/5} \\ \text{loss}=(1)/(5)* x \end{gathered}`

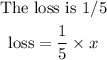
Step 3: Find the expression for the remaining routes

`\begin{gathered} \text{Routes left after loss} \\ x-(1)/(5)* x=x-(x)/(5)=(5x-x)/(5)=(4x)/(5) \end{gathered}`

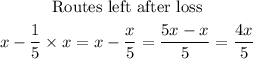
Step 4: Equate the expression for the remaining routes to the given statement in the question

`(4x)/(5)=88`

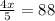
Step 5: Solve the equation to get x

`\begin{gathered} (4x)/(5)=88 \\ 4x=5*88 \\ x=(5*88)/(4) \\ x=5*22 \\ x=110 \end{gathered}`

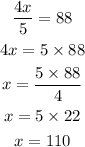
Hence