The probability of 2 consecutive events is the product of the probability of the single events.
The probability of an single event A is the quotient of the number of favorable outcomes to A and the total number of outcomes.
First, let's calculate the probability of picking a 7.
Favorable outcome: 7
Number of favorable outcomes: 1
Total possible outcomes: 7, 8, 9
Number of total outcomes: 3
Then, the probability is of picking a 7:

Second let's calculate the probability that the second card is greater than 7, without putting the first card back.
If the first card was 7, we have the options now: 8, 9.
Favorable outcome: 8, 9
Number of favorable outcomes: 2
Total possible outcomes: 8, 9
Number of total outcomes: 2
Then, the probability is of picking a number greater than 7:
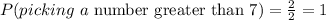
Finally, let's calculate the probability of picking a 7 and then picking a number greater than 7 (without putting the first card back).
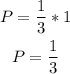
Answer: The probability is 1/3.