Question

The coordinates of the vertices of a polygon are (−2,1), (−3,3), (−1,5), (2,4), and (2,1).What is the perimeter of the polygon to the nearest tenth of a unit?

Answer 1

Given that the coordinates of the vertices of a polygon are (−2,1), (−3,3), (−1,5), (2,4), and (2,1).

Let the vertices are A(−2,1), B(−3,3), C(−1,5), D(2,4), and E(2,1).

We have to find the perimeter of the polygon. The perimeter of the polygon is:

`\text{Perimeter}=AB+BC+CD+DE+EA`

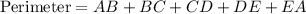
We know that the distance formula is:

`D=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}`

So, the edges of the polygon are:

`\begin{gathered} AB=\sqrt[]{(-2-(-3))^2+(1-3)^2} \\ =\sqrt[]{(-2+3)^2+(-2)^2} \\ =\sqrt[]{(1)^2+4} \\ =\sqrt[]{5} \\ =2.2 \end{gathered}`
`\begin{gathered} BC=\sqrt[]{(-3-(-1))^2+(3-5)^2} \\ =\sqrt[]{(-3+1)^2+(-2)^2} \\ =\sqrt[]{(-2)^2+4} \\ =\sqrt[]{4+4} \\ =2\sqrt[]{2} \\ =2.8 \end{gathered}`
`\begin{gathered} CD=\sqrt[]{(-1-2)^2+(5-4)^2} \\ =\sqrt[]{(-3)^2+(1)^2} \\ =\sqrt[]{9+1} \\ =\sqrt[]{10} \\ =3.2 \end{gathered}`
`\begin{gathered} DE=\sqrt[]{(2-2)^2+(4-1)^2} \\ =\sqrt[]{0+(3)^2} \\ =\sqrt[]{9} \\ =3 \end{gathered}`
`\begin{gathered} EA=\sqrt[]{(2-(-2))^2+(1-1)^2} \\ =\sqrt[]{(2+2)^2+0} \\ =\sqrt[]{16}^{} \\ =4 \end{gathered}`

So, the perimeter of the polygon is:

`\begin{gathered} P=AB+BC+CD+DE+EA \\ =2.2+2.8+3.2+3+4 \\ =15.2 \end{gathered}`

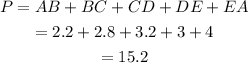
Thus, the perimeter of the polygon is 15.2 units.