Question

Find the relative extrema of the function and classify each as a maximum or minimum. f(x) = (x + 2)2/3 O There are no relative extrema. O Relative minimum: (-2, 0) O Relative minimum: (2,0) Relative maximum: (2,0)

Answer 1

We have the following:

`f(x)=(x+2)^{(2)/(3)}`

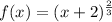
the first thing is to derive the function:

`f^(\prime)(x)=\frac{2}{3\cdot(x+2)^{(1)/(3)}}`

the critical points are points where the function is defined and its derivative is 0 or it is not defined

`\begin{gathered} 3\cdot(x+2)^{(1)/(3)}=0 \\ (3)/(3)\cdot(x+2)^{(1)/(3)}=(0)/(3) \\ (x+2)^{(1)/(3)}=0 \\ x+2=0\rightarrow x=-2 \end{gathered}`

now,we graph and we have

we can see that it is a minimum, therefore the answer is relative minimum (-2, 0)