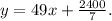To answer this question we will use the following slope-point formula:
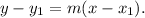
Recall that the slope of the tangent line to the graph of a function h(x) at (x,h(x)) is h'(x).
Now, we know that:
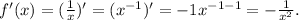
a) Evaluating f'(x) at x=-7 we get:
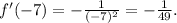
Using the slope-point formula we get that the tangent line to the graph of the function at x=-7 is:
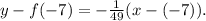
Simplifying the above result we get:
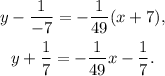
Subtracting 1/7 from the above equation we get:
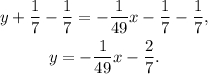
b) Now, recall that the product of the slopes of two perpendicular lines is -1, therefore, the slope of the perpendicular line to the tangent line of the given function at x=-7 is:

Using the slope-point formula we get that:

Substracting 1/7 from the above equation we get:
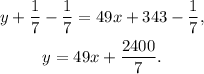
Answer:
(a)
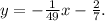
(b)