1 Answer

Marcovtwout · Answer 1 · 2023-10-18T22:26:42+0000

We have to find the probability that a randomly selected a point it falls into the red shaded area:

First, let us find the area of the circle:

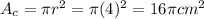
$A_c=\pi r^2=\pi(4)^2=16\pi cm^2$

Now, we can calculate the area of the triangle:

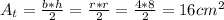
$A_t=(b\ast h)/(2)=(r\ast r)/(2)=(4\ast8)/(2)=16cm^2$

Now, the probability is given by:

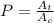
Replacing:

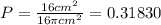
$P=(16cm^2)/(16\pi cm^2)=0.31830$

Multiply the result by 100:

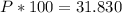
$P\ast100=31.830$

Rounded to the nearest percent P≈32.

Hence, the result is 32%.

Please log in or register to add a comment.