Question

What is the inverse function? Select the correct choice below and fill in the answer box within your choice if necessaryO A. f(x)=OB. The function is not one-to-one.

Answer 1

Given data:

The given expression for the function is f(x)= 5/(x+3).

The expression for one-to-one function is,

`\begin{gathered} (5)/(x_1+3)=(5)/(x_2+3) \\ x_2+3=x_1+3 \\ x_2=x_1 \end{gathered}`

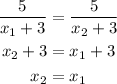
The above expression shows that the given function is one-to-one.

The expressionn for the inverse function is,

`\begin{gathered} y=(5)/(x+3) \\ y(x+3)=5 \\ xy+3y=5 \\ xy=(5-3y) \\ x=(5-3y)/(y) \end{gathered}`

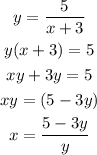
Replace y by x in the above expression.

`f^(-1)(x)=(5-3x)/(x)`

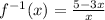
Thus, the given function is one-to-one and the expression for the inverse function is (5-3x)/x .