a)
To determine g(-1) we just need to substitute the value of x=-1 in the function given:
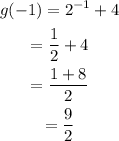
Therefore:
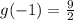
Now, that we have the value of the function we conclude that the point (-1,9/2) is on the graph of g.
b)
In this case we need to find the value of x to do this we equate its expression to 12 and solve for x:
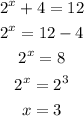
Therefore, if g(x)=12 then x=3 and the point (3,12) is on the graph of g.